• •
王建康*
WANG Jian-Kang*
摘要:
二项分布是广泛存在的一种离散型概率分布。服从二项分布B(n,p)的一个随机变量等于n个相互独立且服从贝努利分布B(1,p)的随机变量之和,二项分布包含参数p的估计与检验等同于贝努利分布参数p的估计与检验。本文修正常见教科书中有关二项分布双边收尾概率计算和假设检验统计量构建中存在的3处问题。(1) 对二项分布的B(n,p)取值概率pk(k=0,1,...,n)从小到大排序,排序后的概率用p(k)表示,观测值k的双边收尾精确概率等于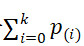 ;(2) 二项分布B(n,p)参数p与给定值p0的差异显著性检验统计量被修正为
;(2) 二项分布B(n,p)参数p与给定值p0的差异显著性检验统计量被修正为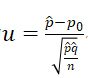 ,该统计量在大样本条件下近似服从正态分布N(p-p0,1);(3) 二项分布B(n1,p1)和B(n2,p2)的参数p1和p2差异显著性检验统计量被修正为
,该统计量在大样本条件下近似服从正态分布N(p-p0,1);(3) 二项分布B(n1,p1)和B(n2,p2)的参数p1和p2差异显著性检验统计量被修正为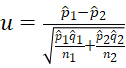 ,该统计量在大样本条件下近似服从正态分布N(p1-p2,1)。修正后的双边收尾概率是精确值,不会出现概率大于1的问题。修正后的2个检验统计量无论原假设是否成立,其大样本近似正态分布的方差均为1,有利于准确研究备择假设条件下检验统计量的功效。此外,文中还介绍了小样本条件下二项分布参数的精确检验,对比分析了准确检验与近似检验的异同;讨论了修正统计量的理论基础,给出了小概率和大样本的判定标准,列出了贝努利分布参数检验与正态分布均值检验的异同。期望读者能够从中了解到假设检验与统计推断作为统计学核心研究内容的全貌。
,该统计量在大样本条件下近似服从正态分布N(p1-p2,1)。修正后的双边收尾概率是精确值,不会出现概率大于1的问题。修正后的2个检验统计量无论原假设是否成立,其大样本近似正态分布的方差均为1,有利于准确研究备择假设条件下检验统计量的功效。此外,文中还介绍了小样本条件下二项分布参数的精确检验,对比分析了准确检验与近似检验的异同;讨论了修正统计量的理论基础,给出了小概率和大样本的判定标准,列出了贝努利分布参数检验与正态分布均值检验的异同。期望读者能够从中了解到假设检验与统计推断作为统计学核心研究内容的全貌。
| [1] DeGroot M H, Schervish M J. Probability and Statistics (4th edn). Pearson Education Asia Ltd. and China Machine Press, 2012. [2] 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程(第2版). 北京: 高等教育出版社, 2011. Mao S S, Cheng Y M, Pu X L. Course on Probability Theory and Mathematical Statistics, 2nd edn. Beijing: Higher Education Press, 2011 (in Chinese). [3] 刘来福, 程书肖. 生物统计. 北京: 北京师范大学出版社, 1988. Liu L F, Cheng S X. Biometrics. Beijing: Beijing Normal University Press, 1988 (in Chinese). [4] 李仲来, 刘来福, 程书肖. 生物统计(第2版), 北京师范大学出版社, 2007. Li Z L, Liu L F, Cheng S X. Biometrics, 2nd edn. Beijing: Beijing Normal University Press, 2007 (in Chinese). [5] 南京农业大学. 田间试验和统计方法(第2版). 北京: 农业出版社, 1991. Nanjing Agricultural University. Field Experiments and Statistical Methods, 2nd edn. Beijing: Agriculture Press, 1991 (in Chinese). [6] 盖钧镒, 管荣展. 试验统计方法(第5版). 北京: 中国农业出版社, 2020. Gai J Y, Guan R Z. Experimental and Statistical Methods, 5th edn. Beijing: China Agriculture Press, 2020 (in Chinese). [7] 明道绪. 田间试验与统计分析(第3版). 北京: 科学出版社, 2013. Ming D X. Field Experiments and Statistical Analysis, 3rd edn. Beijing: Science Press, 2013 (in Chinese). [8] 刘永建, 明道绪. 田间试验与统计分析(第4版). 北京: 科学出版社, 2020. Liu Y J, Ming D X. Field Experiments and Statistical Analysis, 4th edn. Beijing: Science Press, 2020 (in Chinese). [9] Hogg R V, McKean J W, Craig A T. Introduction to Mathematical Statistics (7th edn). Pearson Education Asia Ltd. and China Machine Press, 2012. [10] 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程习题与答案. 高等教育出版社, 2005. Mao S S, Cheng Y M, Pu X L. Exercises and Answerers to the Course on Probability Theory and Mathematical Statistics. Beijing: Higher Education Press, 2005 (in Chinese). [11] Fisher R A. Statistical Methods, Experimental Design, and Scientific Inference. Oxford Science Publications, Reprinted, 2003 [12] Weir B S. Genetic Data Analysis II. Sinauer Associates, Inc., Sunderland, Massachusetts, 1996 [13] 王建康. 数量遗传学. 北京: 科学出版社, 2017. Wang J K. Quantitative Genetics. Beijing: Science Press, 2007 (in Chinese). [14] 《数学手册》编写组. 数学手册. 北京: 高等教育出版社, 1979. Writing Group of the Mathematics Manual. Mathematics Manual. Beijing: Higher Education Press, 1979 (in Chinese). [15] 茆诗松, 王静龙, 濮晓龙. 高等数理统计(第2版). 北京: 高等教育出版社, 2006. Mao S S, Wang J L, Pu X L. Advanced Mathematical Statistics, 2nd edn. Beijing: Higher Education Press, 2006 (in Chinese). |
| No related articles found! |
|
||